The Micromeritics SediGraph is designed to provide particle size distribution analyses for materials based upon sedimentation of the particles through a liquid of known viscosity and density. Stokes’ Law is used to determine the equivalent spherical diameter of the settling particle from its terminal velocity or sedimentation velocity, v. The velocity is based upon the maximum distance that particles have settled, h, and the elapsed time of the analysis, t. The known density, ρo, and viscosity, η, of the suspending liquid, and the apparent skeletal density, ρ, of the settling particles are provided at the start of the analysis. The acceleration due to gravity, a constant, g, is the remaining calculation parameter. Thus Stokes’ Law, as implemented by the SediGraph, solved for particle diameter, dp, is given by equation (1).
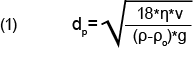
It was shown by Stokes that the drag coefficient is essentially independent of the particle velocity for slowly moving particles. For particles moving with velocities within the regime of laminar flow, generally applicable for low Reynolds Numbers, Re ≤ 0.3, as given in equation (2), this assumption holds well, and results in a calculated particle diameter with an uncertainty of less than 3%
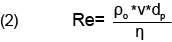
Note that the Reynolds number increases with the cube of particle diameter, since the particle velocity increases with the square of the particle diameter. Therefore the particle settling with the highest velocity will be the largest particle present in the sample. To help ensure that all particles present in the sample settle with a Reynolds Number less than 0.3, and thus within the desired laminar flow regime, a suspending fluid with a viscosity sufficient to limit the settling velocity of the largest particle present to the laminar flow regime is required. Combining equations (1) and (2) and restricting the Reynolds Number to 0.3, equation (3) can be used to calculate the minimum viscosity needed, ηmin, needed to support the largest particle present, dmax, so as to settle with a Reynolds Number of 0.3.
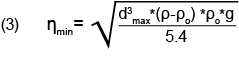
Note that some conversion factors, such as powers of ten, may be needed when customary units are used, such as centipoise for viscosity, micrometers for particle diameter, and cubic centimeters per gram for densities.
Values for the minimum viscosity needed to support particles of different maximum diameter for a variety of common materials are listed in Table 1. The density of the suspended liquid in these calculations is that of water at 35°C. These materials are selected so as to provide values over a wide range of particle skeletal density values. In this table, the units used are those customary ones mentioned above. Combinations of maximum diameter and particle density that indicate that a liquid with a viscosity greater than that of water at 35°C are shown highlighted in green. Those that indicate that the minimum viscosity needed is less than that of water at 35°C are shown highlighted in blue. Note then that water can be used for these latter cases, those with blue highlight, whereas the viscosity of water will need to be modified, such as with addition of glycerol or sucrose, in the former cases, those with green highlight.
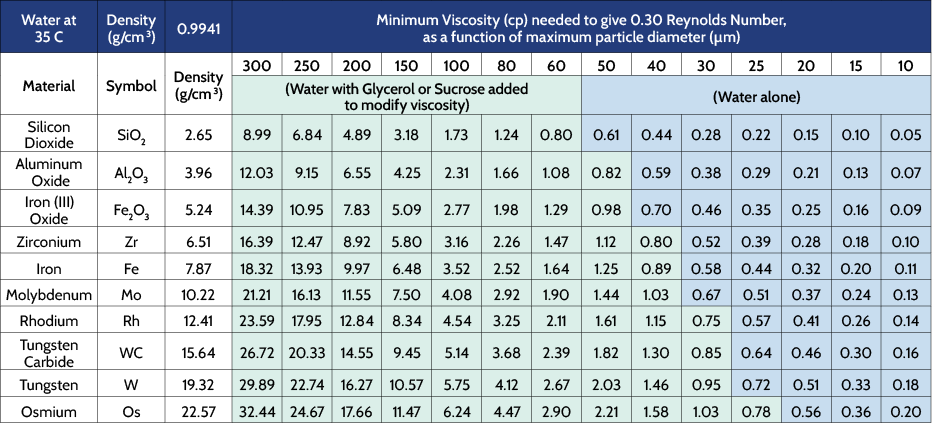
Table 2 shows the largest particle, for a variety of materials, having a Reynolds Number of 0.3 when suspended in different aqueous solutions, where the liquid viscosity has been modified by the addition of glycerol or sucrose. The percentages shown are the mass of modifier added as a percentage of mass of the final solution, that is, on a (w/w) basis.
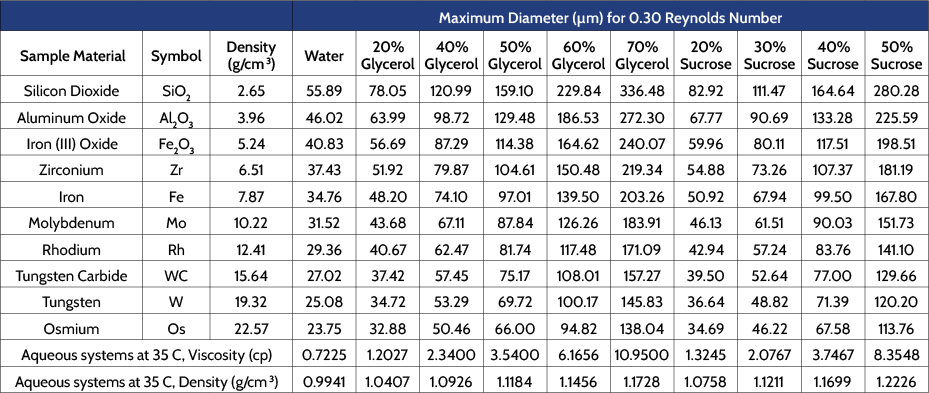
Table 3 contains similar information as Table 2, this time for a variety of organic liquids commonly used as suspending media. Note that the viscosity for some of these are quite small, and so can only be used to adequately suspend small particles under analysis.
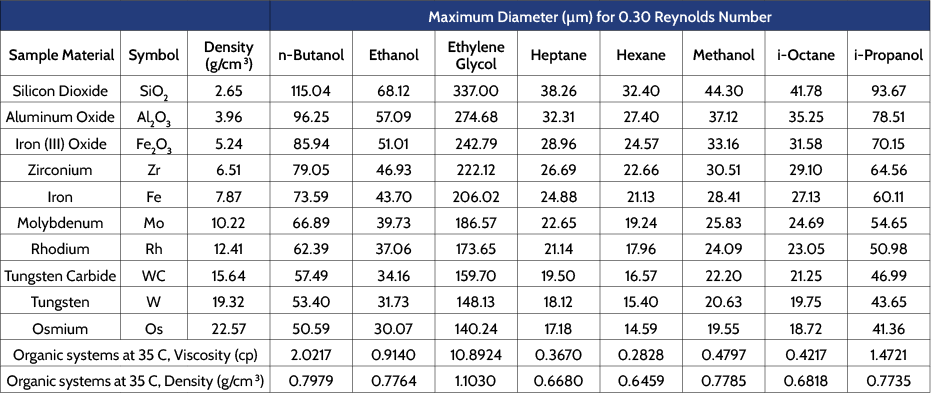
Micromeritics manufactures a range of dispersing media for use with the SediGraph when performing sedimentation particle size analysis. Most of these SediSperse media are organic-based, with appropriate surfactants added to stabilize the dispersion, useful when analyzing materials that react with or that dissolve in water. Two are aqueous systems, W-11 and W-12, which utilize non-ionic surfactants to help stabilize the dispersion. Table 4 contains the maximum particle size that can be analyzed for a variety of materials when suspending in typical lots of the available SediSperse media.
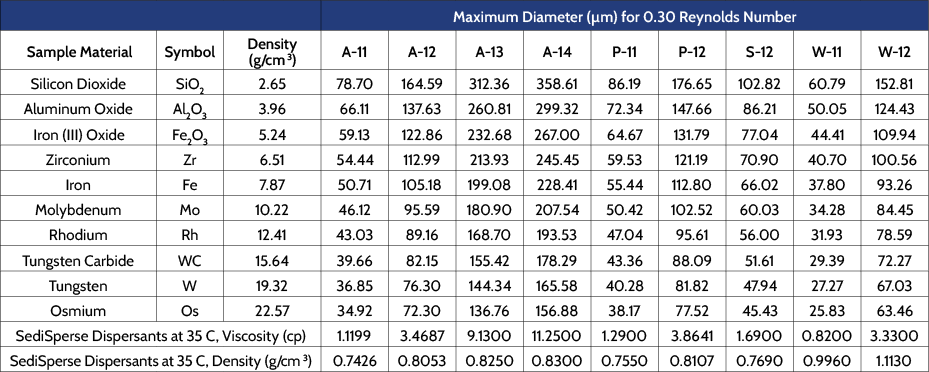
As can be seen, the viscosity of the suspending media is one of the critical factors when performing sedimentation particle size analysis using the SediGraph. A variety of means for obtaining adequately supporting viscosity are provided for a variety of sample materials, including the use of SediSperse media manufactured by Micromeritics. Failure to have adequate viscosity to support the largest particle present can result in error in particle diameter calculated using Stokes’ Law.