
Sedimentation analysis based upon Stokes’ Law provides a convenient method for determining particle size distribution (PSD). A single solid (or nonporous) sphere settling in a fluid has a terminal settling velocity which is uniquely related to its diameter. The SediGraph determines particle size distributions using the sedimentation method. By measuring the gravity-induced settling velocities of different size particles in a liquid with known properties, the particle sizes are determined. The rate at which nonporous particles fall through a liquid is described by Stokes’ Law as
Dst = [18ηV/(ρs – ρ1)g]1/2
Dst = Stokes’ diameter
η = fluid viscosity
ρs = density of the solid
ρ1 = density of the liquid
V = settling velocity
g = acceleration due to gravity
The measured particle size distribution is a function of the particle skeletal density. The skeletal density is defined as the mass of discrete pieces of solid material divided by the volumes of the pieces and closed (or blind) pores within the pieces. Such information is easily obtained with a helium pycnometer. However, for most pure materials the handbook value for density is quite sufficient.
A fully wetted porous particle settling in a liquid has an effective density different from the skeletal density. The effective density is a linear combination of the particle percent porosity times the density of the fluid plus (100% – % porosity) times the particle skeletal density. In the form of an equation, this statement becomes
ρes = [P – ρf + (100 – P)ρs/100]
ρes = effective sedimentation density for a particle with open pores
P = percent open porosity of the particle
ρf = density of sedimentation fluid
ρs = skeletal density of the nonporous particle
A powdered Si/Al catalyst substrate serves as a good example. The skeletal density of this material is 2.60 g/cm3. The SediGraph particle size distribution is shown in Figure 1.
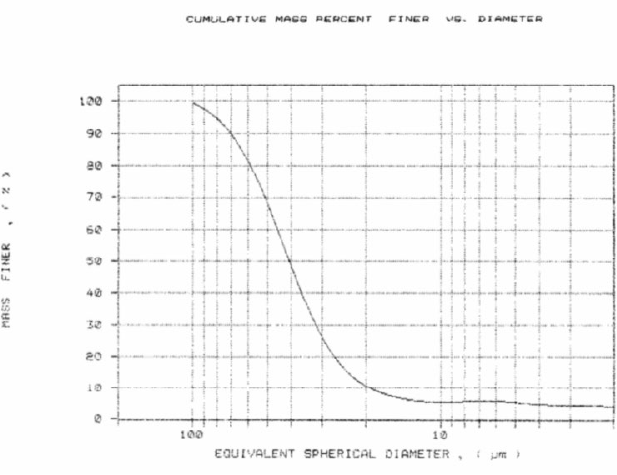
This analysis assumed the particle to be nonporous. Actually the material is 59% porous. In order to obtain an accurate PSD, the sedimentation density must be changed to 1.65 g/cm3. This is calculated as follows: Sedimentation Density = 59%(0.99 g/cm3 ) + 41%(2.60 g/cm3 ) = 1.65 g/cm3 where 0.99 g/cm3 is the density of the sedimentation fluid (in this example, water at 35 °C) which occupies the pore volume of the powder and 41% is the solid volume of the settling particle of the known skeletal density of 2.60 g/cm3. Figure 2 shows the SediGraph PSD obtained using an effective sedimentation particle density of 1.65 g/cm3 compared to the curve of Figure 1.
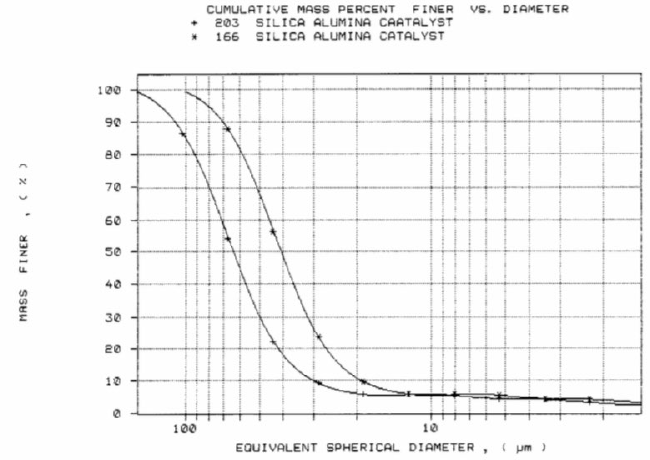
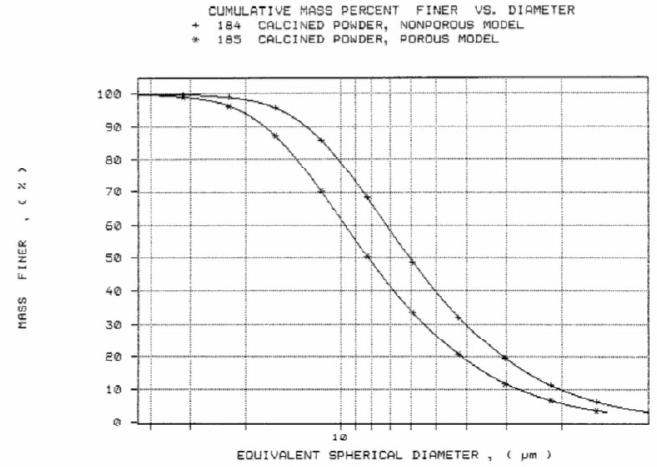
Using a density of 1.65 g/cm3 yielded a coarser particle size distribution. The mass median diameter, d50, increased from 40.9 to 64.0 mm (micrometers). SediGraph particle size distributions are important quality control tools for powder processing. As indicated by the curves shown in Figure 2, SediGraph particle size analysis of porous powders must involve density correction for the powder porosity. This fact can be crucial to the production control of porous aluminas from alumina trihydrate (ATH). ATH is a nonporous powder with a skeletal density of 2.42 g/cm3. Calcination of ATH causes loss of water with a resultant increase in skeletal density and the creation of porosity. A sample of ATH and the calcined product derived from it were analyzed on the AccuPyc, SediGraph, and AutoPore. The calcined product showed a skeletal density of 2.9265 g/cm3 and a 35% porosity.
| Material | Density (g/cm3) | Mass Median Diameter (mm) |
| ATH | 2.42 | 8.12 |
| Calcined | 2.926 | 6.07 |
| Calcined (35% porous) | 2.05 | 8.21 |
Figure 4 displays the two curves of Figure 3 overlaid with the SediGraph Particle Size Distribution of the original ATH. The mass median diameter of the ATH was 8.12 mm. The curve for the calcined material (35% porous) overlays the ATH curve almost exactly
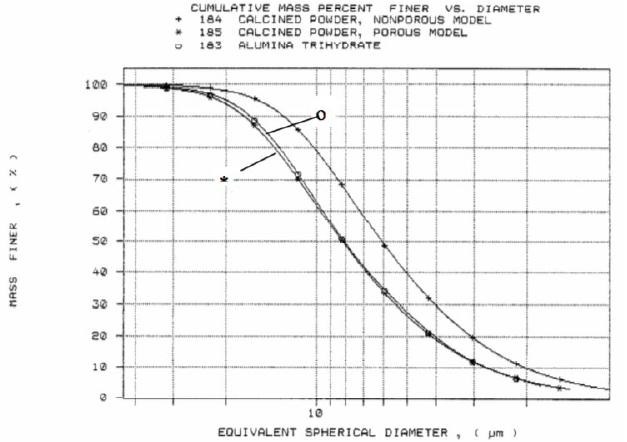
The calcination of ATH should not greatly alter the particle size distribution of the resultant product. If the porosity generated by the process is not included in the analysis, then it appears that the calcination has indeed altered the particle size distribution; this is known to be untrue. If the porosity of the calcined product is taken into account in the particle size analysis, then the calcined product is seen to have the same particle size distribution as the starting material. The percent porosity of any powdered material can be obtained quickly using mercury intrusion porosimetry, as discussed in Micromeritics’ Application Note No. 83.