Abstract
The chemical adsorption isotherm reveals information about the active surface of a material and has been employed for many years as a standard analytical tool for the evaluation of catalysts. Temperature-programmed reaction techniques have emerged from the 1950’s as an indispensable companion to chemisorption isotherm analyses in many areas of industry and research. This paper provides an introduction to these analytical techniques.
Introduction
Optimum design and efficient utilization of catalysts require a thorough understanding of the surface structure and surface chemistry of the catalytic material. Chemical adsorption (chemisorption) analyses can provide much of the information needed to evaluate catalyst materials in the design and production phases, as well as after a period of use. The required analytical equipment can be relatively inexpensive, simple to operate, and fast compared to alternate equipment capable of obtaining the same information.
Differentiating Physical and Chemical Adsorption
A solid material usually exhibits a heterogeneous distribution of surface energy. Gas, vapor, or liquid molecules may become bound to the surface if they approach sufficiently close to interact. The discussions in this paper are confined to the adsorption (and desorption) of gases or vapors on (or from) solid surfaces. The solid is called the adsorbent; the gas or vapor molecule prior to being adsorbed is called the adsorptive and while bound to the solid surface, the adsorbate.
Physical adsorption is the result of a relatively weak solid-gas interaction. It is a physical attraction resulting from nonspecific, relatively weak Van der Waal’s forces and adsorption energy usually not exceeding 80 kJ/mole, with typical energies being considerably less. Physically adsorbed molecules may diffuse along the surface of the adsorbent and typically are not bound to a specific location on the surface. Being only weakly bound, physical adsorption is easily reversed.
Adsorption also can result in a surface complex, a union much stronger than a physical bond with heats of adsorption up to about 600 kJ/mole for C-N bonds and 800 kJ/mole for chemical bonds. A chemical bond involves sharing of electrons between the adsorbate and the adsorbent and may be regarded as the formation of a surface compound. Due to the bond strength, chemical adsorption is difficult to reverse.
Physical adsorption takes place on all surfaces provided that temperature and pressure conditions are favorable. Chemisorption, however, is highly selective and occurs only between certain adsorptive and adsorbent species and only if the chemically active surface is cleaned of previously adsorbed molecules.
Under proper conditions, physical adsorption can result in adsorbed molecules forming multiple layers. Chemisorption, in the typical case, only proceeds as long as the adsorptive can make direct contact with the surface; it is therefore a single-layer process. Exceptions can exist if the adsorptive is highly polar such, NH3 being an example. Both physical and chemical adsorption may occur on the surface at the same time; a layer of molecules may be physically adsorbed on top of an underlying chemisorbed layer. The same surface can display physisorption at one temperature and chemisorption at a higher temperature. For example, at liquid nitrogen temperature (77 K) nitrogen gas is adsorbed physically on iron but at 800 K, an energy level too high for physical adsorption bonds, nitrogen is adsorbed chemically to form iron nitride (Moore).
General Applications of Gas Sorption as Analytical Tools
A variety of surface features can be determined from observations of the adsorption process. The quantity of molecules taken up by a surface depends on several variables including temperature, pressure, surface energy distribution, and the surface area and porosity of the solid. The relationship between the quantity of molecules adsorbed and the pressure at constant temperature is called the adsorption isotherm.
Physical adsorption and desorption isotherms are important in characterizing the overall surface. The slightest change in the shape of the plotted isotherm is indicative of a particular surface feature. Analyses of physical adsorption isotherm data reveal the total surface area, mesopore and micropore volume and area, total pore volume, the distribution of pore volume and area by pore size, and surface energy distribution. Thus, physical adsorption is an important tool in the study of catalysts, particularly in evaluating the support structure.
The chemical adsorption isotherm also evaluates the surface, but is selective in that it only probes the active areas—those capable of forming a chemical bond with the adsorptive gas or vapor. This selectivity involves both the probe molecule and the molecular or atomic composition of the active material, so the choice of probe molecules is much more important in chemisorption tests. Although isothermal chemisorption tests are important in characterizing active surfaces, temperature-programmed tests are even more so. The basic form of data produced by these tests resembles a chromatogram of temperature versus quantity desorbed.
Catalyst Basics
A catalyst affects the rate of a chemical reaction. ‘Rate’ is the most important word in this description because a catalyst cannot induce a reaction that is not permissible under the laws of thermodynamics. A catalyst only can increase the rate at which the reaction approaches equilibrium.
Heterogeneous catalysts include metals, metal oxides and solid acids. Pure metals may be employed as solid catalysts, or may be dispersed as small grains on the surface of a supporting material such as TiO2, ZrO2, Al2O3, or SiO2. The preparation of a supported catalyst involves selecting precursors of the active components and any necessary promoters and mixing them in a solvent. The mixture forms a precipitant, or is used to coat an inert carrier, or is used to impregnate a carrier. Ultimately, the active metal or precursor is dispersed on the carrier. The product is dried, mixed with a binder or forming agent, then ground, pelletized, extruded, or otherwise shaped. Finally, the material is calcined and activated by oxidation, reduction, or other means.
One type of unsupported catalyst is composed of pure metal. Raney metal catalysts, for example, are prepared by dissolving an aluminum-nickel alloy in a solution of sodium hydroxide, which dissolves the aluminum component. The end product is a highly porous active metal ‘sponge’, all other scaffolding materials having been removed. Another unsupported metal catalyst is produced by fusing or sintering metal oxides with promoters, thus forming a network of pores throughout the metal mass (van der Laan). An example of this is a fused iron ammonia synthesis catalyst.
Zeolitic catalysts form another group. Zeolites are hydrated aluminosilicates and are used widely in the chemical industry and refining operations. Their activity is influenced by the silica to alumina ratio. Amorphous silica-alumina catalysts have a lower activity than zeolitic catalysts and are applied in mild hydrocracking operations. An acidic surface is required for cracking and the acidity is associated with the oxygen atoms attached to aluminum atoms.
Chemisorption and Catalysts
The catalytic process can be generalized by a short sequence of steps as follows. Consider reactant molecules A and B in the gaseous bulk above a solid surface that supports an ensemble of active metal sites S. If molecule A is chemically adsorbed on one of the active sites, a surface complex A is formed. Next, A reacts with B forming molecule A+B, which escapes the site, thus regenerating site S.
Sorption of at least one of the reactant molecules is required for catalysis to occur. If the accelerated rate of reaction simply was due to the concentration of molecules at the surface, catalysis would result from physical adsorption of the reactants. Chemisorption is a essential step, the adsorbed molecule forming an intermediate surface complex that is more receptive to chemical reaction. The dependence of catalysis on chemisorption is one reason why chemisorption is such an informative analytical technique in the study of catalysis—the chemistry occurring in the application of the catalyst is being observed directly in the laboratory.
The performance of a catalyst depends on several variables. First, adsorption sites must be both numerous and available to the reactant molecules. In some cases, grains of active metal are at the surface, but there also are grains located below the surface and unavailable to the reactants. Adsorption sites simply being located on the surface is insufficient to assure optimum performance. For example, some potential adsorption sites may be located deep within a micropore that is too narrow for the reactant molecule to enter or for the reaction product to exit; in this case the surface site cannot be an active participant in chemisorption. A site could be located along a tortuous path that impedes the efficient flow of reactants toward the active site and products away from the site. Since many active metals are very expensive, an important design criterion is to maximize the number of active sites per unit of metal.
Catalytic activity depends on how rapidly chemisorption occurs and the strength (energy) of the chemisorption bond. If the bond is too weak, the molecule may desorb prior to reacting; if too strong, the release of the product and regeneration of the site may be retarded. Isothermal chemisorption methods as well as temperature-programmed chemisorption methods can be used to study surface energy distribution.
Chemisorption as described above pertains to the use of catalysts in various applications. The same reactions, only on a smaller scale, also can occur in a sample tube under controlled conditions allowing the process to be studied. This is chemisorption used as an analytical technique. Chemisorption analyses are applied to physically characterize a catalyst material, to determine a catalyst’s relative efficiency in promoting a particular reaction, to study catalyst poisoning, and in monitoring the degradation of catalytic activity over time of use. Among the various instrument techniques used in analyzing catalysts, chemisorption techniques are the most universally employed.
Chemisorption Instruments
Isothermal chemisorption analyses are obtained by two chemisorption techniques: a) static volumetric chemisorption, and b) dynamic (flowing gas) chemisorption.
The volumetric technique is convenient for obtaining a high-resolution measurement of the chemisorption isotherm from very low pressure to atmospheric pressure at essentially any temperature from near ambient to 1000+ oC. Commercial embodiments of this technique are almost exclusively automated. Obtaining a high-resolution isotherm requires many, precise dosing steps in pursuit of the equilibrium point, and many pressure steps which, without automation, would be a time-consuming and error prone procedure.
The flowing gas (dynamic) technique operates at ambient pressure. After the sample has been cleaned, small injections (doses) of accurately known quantities of adsorptive are administered in pulses until the sample is saturated, thus the name, ‘pulse chemisorption’. A calibrated thermal conductivity detector (TCD) monitors the quantity of adsorptive that is not taken up by active metals. This quantity is subtracted from the injected quantity yielding the quantity adsorbed from each injection. These are summed to determine the capacity of the sample mass. Injections may be made by syringe or by a manual or automated HPLC-type, loop injection valve. Since the endpoint (saturation) is the only point measured, the number of injections may be only a few and there are no pressure changes. Thus, the flowing-gas technique is often performed manually, although automated instruments also are available.
Over the past few decades, temperatureprogrammed chemisorption analyzers have become recognized as extremely valuable tools for characterizing catalysts. The method is sometimes simply referred to as temperature-programmed reactions, and includes Temperature-Programmed Desorption (TPD), Temperature Programmed Reduction (TPR) and Temperature Programmed Oxidation (TPO). The dynamic chemisorption method is particularly suitable to performing temperature program analyses.
Chemisorption Analyses
The versatility of the chemisorption technique is illustrated by the extent of information about a material that can be acquired. Some of its versatility has been revealed in the discussion above. In the following sections, additional capabilities are explored.
In the examples that follow, only catalysts composed of a single active species are considered to simplify the math. In the case of mixed metal catalysts, many of the equations below would require summing a series of terms, one for each adsorbing species and each term weighted by the fractional contribution of the species to the whole.
The Chemisorption Isotherm
An isotherm is a set of quantity-adsorbed versus pressure data points that characterize the adsorption process at a constant temperature. To understand this better, consider a reactor of constant volume V that contains a sample and a quantity of gas molecules N. Chemisorption theory assumes that the active surface of a solid contains a fixed number Ns of adsorption sites and only one molecule at a time can occupy a site. The molecules in the sample tube that are competing for an adsorption site represent a concentration C that can be expressed in general by solving the gas law , or
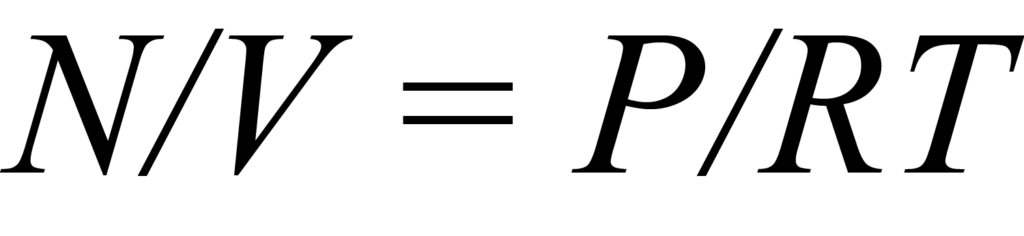
where N and V have previously been defined, P is pressure, T temperature, and R the gas constant.
For a specific gas-solid system at equilibrium under specific conditions of temperature and pressure, a certain fraction ϑ of the total number of available sites Ns will be occupied by nads adsorbed molecules. This is described by
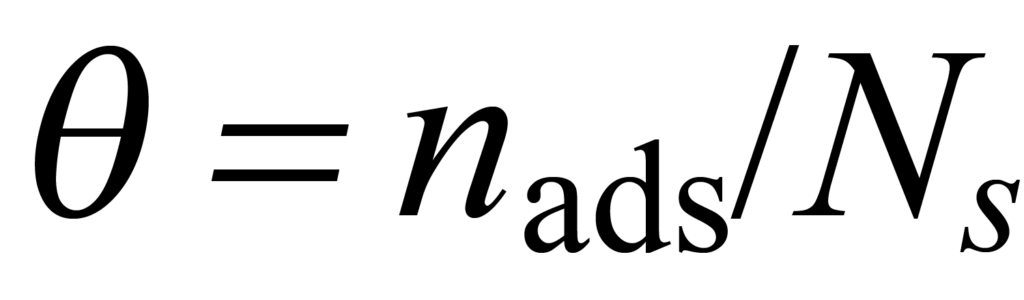
The rate at which equilibrium is achieved depends on the concentration of molecules involved as well as other considerations, the latter being grouped into a parameter referred to as the ‘rate constant’ k.
For the adsorption process, the concentration of unadsorbed molecules competing for the remaining sites is C-ϑC and the rate of adsorption is kads(C-ϑC) or kadsC (1-ϑ). For desorption the fraction of molecules desorbed is ? and the rate of desorption is kdesϑ. When equilibrium is achieved, the rate of adsorption and desorption are equal, that is,
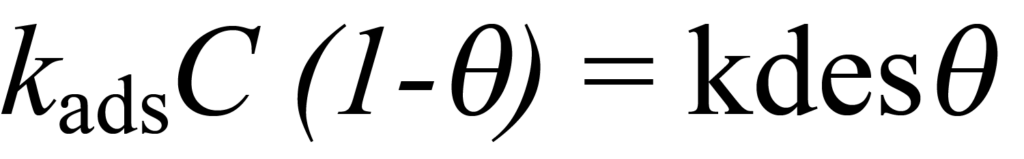
or
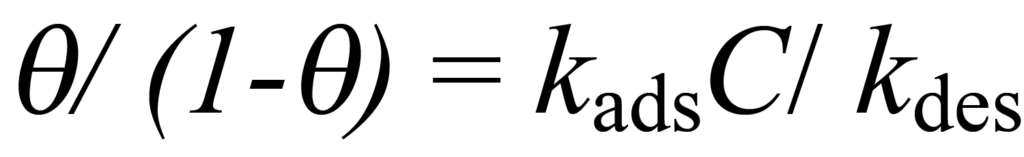
Using K to represent kads/kdes and solving for ϑ yields
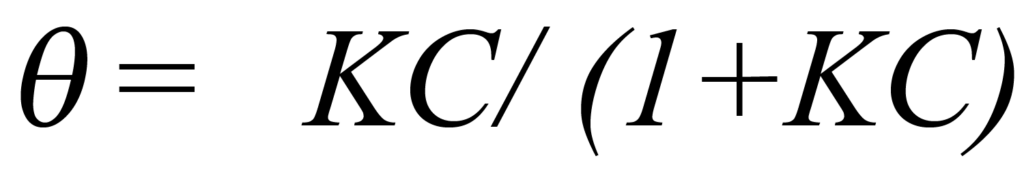
Recalling that the environment is of constant volume V and constant temperature T, changing pressure is the only remaining way to change concentration C. Eq. 1 establishes that concentration is directly proportional to pressure, therefore if concentrationpressure proportionality constant is combined with K and represented by b, Eq.4 can be written
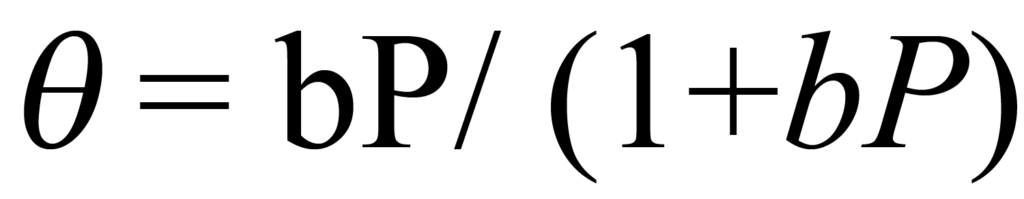
This is the famous Langmuir isotherm, which accurately describes most chemisorption isotherms not involving fragmenting (dissociation) of the adsorptive molecule. The isotherm is asymptotic to ϑ = 1, which is full coverage, or completion of the monolayer.
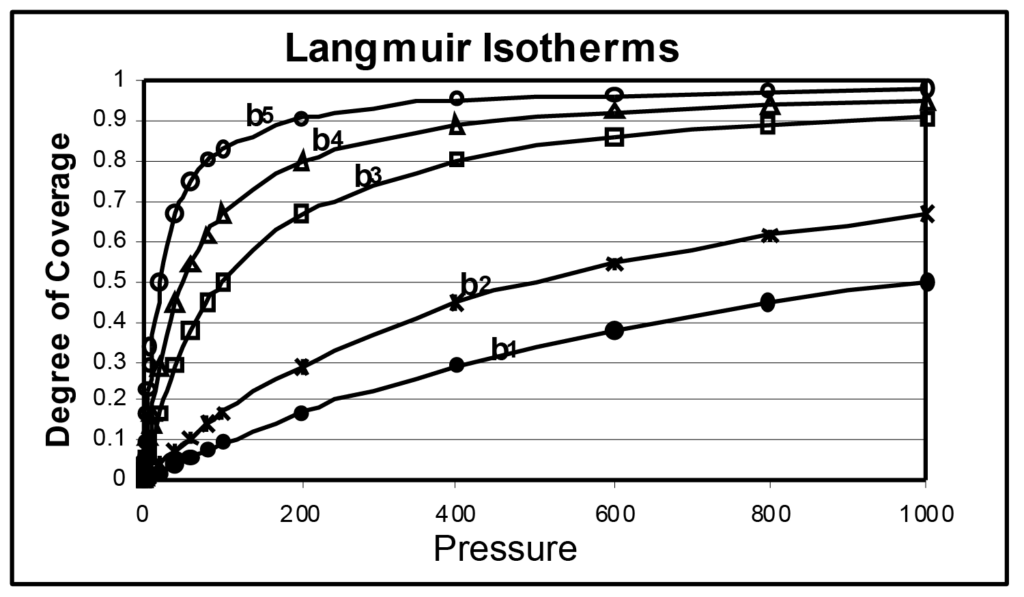
Several Langmuir isotherms are illustrated in Figure 1, the only difference being the magnitude of b. The b parameter is directly related to surface energy; increasing surface energy increases the probability of adsorption at a given pressure. The b parameter is inversely related to temperature, which, when increased, increases molecular energy and decreases the probability of adsorption at a given pressure.
In the illustration, b1 is less than b2, which is less than b3, and so on, b5 being 50 times greater than b1. From this one it may be inferred that the same sample being analyzed at five different temperatures would produce a similar set of isotherms, as would five different samples of different surface energy measured at the same analytical temperature.
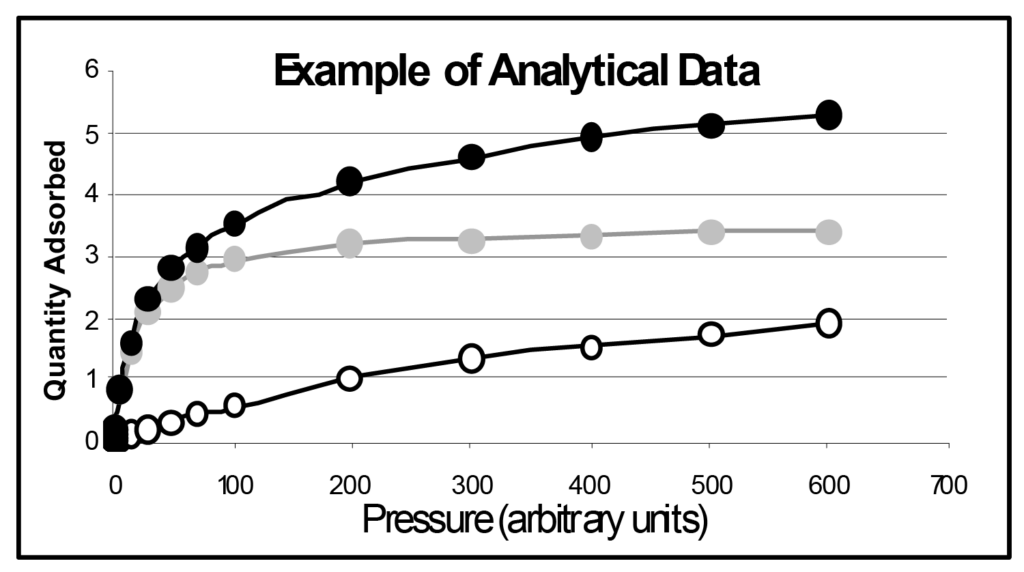
Obtaining a chemisorption isotherm is not necessarily a direct measurement as illustrated in Figures 2. In the typical case indicated by these illustrations, there will be molecules (indicated by R) weakly adsorbed to the surface of the support and there also will be a chemisorbed monolayer of molecules (indicated by I) on the active surface. Depending on the pressure and temperature, there also can be molecules physically adsorbed on top of the chemisorbed monolayer.
Weak adsorption is termed reversible adsorption and strong chemisorption, irreversible, thus the R and I labels in the illustration. The initial isotherm will be a combination of reversible and irreversible adsorption.
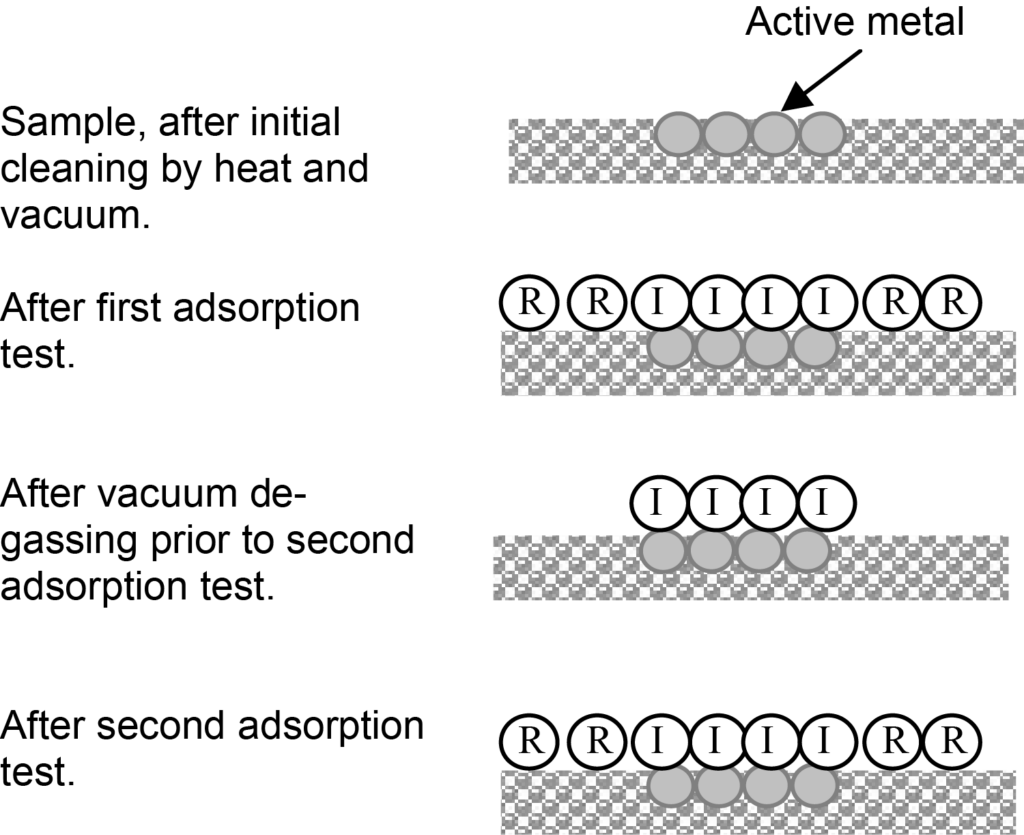
The reversible and irreversible contributions to a combined isotherm can be distinguished by running a second adsorption test. After the initial adsorption test and prior to the second test, the sample is subjected to vacuum only, causing the weakly adsorbed molecules to desorb, leaving only those molecules that have formed a strong chemisorption bond with the active surface.
The second adsorption test is performed under the same conditions as the initial test, but this time the active surface is already covered with a chemisorbed monolayer. The uptake of adsorbate will be only that associated with reversible adsorption. Subtracting the quantity reversibly adsorbed from the combined isotherm at each pressure value yields an isotherm of ireversible adsorption. The analytical results are illustrated in Figure 3.
Number of Accessible Active Sites
Both static volumetric and dynamic chemisorption techniques can be used to measure the quantity of gas required to form a monolayer of chemisorbate on an active surface. The dynamic method yields only a single data point, which corresponds to the quantity of adsorptive required to saturate the active surface with a monolayer. The monolayer capacity of the active surface is calculated from the derived irreversible adsorption isotherm illustrated in Figure 3. Since the irreversible adsorption isotherm is asymptotic to the value of total coverage (of the active surface), the plateau of the isotherm is extrapolated back to the y-axis to yield the monolayer capacity value. Extrapolating to the y-axis the linear section of the combined reversible-irreversible isotherms also provides a reasonable value for the monolayer coverage quantity.
The dynamic chemisorption method requires (manually or automatically) injecting small, precisely- known quantities of adsorptive into a stream of inert carrier gas that flows through the sample bed.
The partial pressure of the adsorptive momentarily increases over the sample as the pulse passes and some or all of the injected quantity of gas is adsorbed. Any unadsorbed gas is swept through the detector where it is registered. Note that, unlike the static method (described above), the net adsorption is only irreversible adsorption because, after the pulse of adsorptive passes, the partial pressure of the adsorptive in the bulk gas is essentially zero and escaping weakly adsorbed molecules are swept to the detector by the carrier stream.
As the monolayer forms on the active surface, less and less of the injected adsorptive is taken up by the sample. Injections continue until the sample is saturated, as indicated when all subsequent detector peaks remain the same size. The results of such a test are shown in Figure 4, which illustrates the output of the detector. The area of each peak is proportional to the quantity of the injection that was not adsorbed.
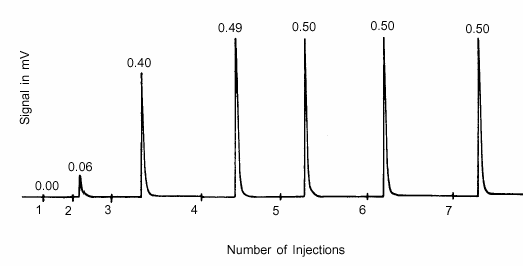
In Figure 4, the integrated area of peaks associated with injections 5, 6, and 7 indicate that no adsorption occurred, so the active area is saturated. All of the first injection was adsorbed, as was 88% of injection 2, 20% of injection 4, and 2% of injection 3. From the known quantity of each injection, the fraction of each injection that was adsorbed, and the mass of sample material, the number of moles of adsorptive gas taken up by each gram of sample is determined.
The adsorption process can involve the separation of a molecular adsorptive into two or more molecular or atomic entities (ions or radicals), each entity forming a bond with individual active surface sites. This is called dissociative or second-order adsorption in contrast to first-order or non-dissociative adsorption in which the adsorptive molecule remains intact during adsorption. The result of dissociative adsorption is that the number of adsorptive molecules Nm determined to have been taken up per gram of sample does not equal the number of active surface atoms that participated in chemisorption.
To determine the number of surface atoms involved, the stoichiometry of the surface reaction must be considered. Stoichiometry refers to the relationship between the amounts of substances that react together in a particular chemical reaction, and the amounts of products that are formed. For example, a hydrogen molecule (H2) may dissociate into two hydrogen atoms and react with two active surface atoms, as is the case with Pt. So, the number of adsorptive molecules taken up by the active surface must be multiplied by a stoichiometry factor Fs (where Fs = 2 in the example case) to arrive at the number of surface atoms Ns or ‘sites’. Mathematically,
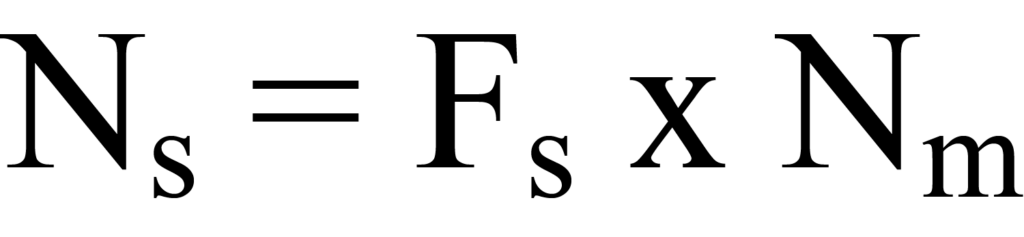
where Ns and Nm are determined per gram of sample.
The adsorptive molecule may be able to bond in more than one configuration with the active surface. The proportion of molecules bonding in each possible way must be taken into consideration, often yielding a non-integer stoichiometry factor.
Active Surface Area
The specific active surface area follows from the number of molecules Ns adsorbed on the active surface of one gram of sample. Specific active surface area AA is determined by multiplying the area Am occupied by one surface molecule by the number of adsorbed molecules per gram Ns. The area occupied by a single atom originating from the adsorptive usually can be located in the literature. It also can be determined experimentally, if necessary, by determining the BET surface area of a sample of pure active material using N2, then determining the molar uptake of the active adsorptive on the same sample.
Metal Dispersion and Percent Metal
Metal dispersion describes the ratio of the number of active metal atoms available for reaction to the total number of metal atoms in the catalyst material. The quantity of active metal incorporated per unit mass of support material is available from the manufacturing formula; this will yield the quantity of active metal atoms NT per unit mass of catalyst. Chemisorption analysis as described above is used to determine the quantity of active metal per gram that is available for reaction. The percent dispersion is the ratio of the available quantity to total quantity of active molecules times 100%, or
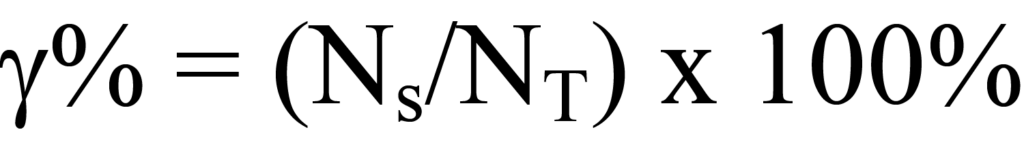
Dispersion is expressed as a ratio of available metal to total metal. Another fraction that is determined from the manufacturing procedure is the ratio of the weight of metal to the mass of the bulk catalyst material, expressed as a decimal fraction or as a percentage.
Active Particle (Crystallite) Size
This estimation of active particle size is a geometrical calculation based on the assumption that the crystallite shape is of regular geometry, a sphere typically being the geometry of choice. What is known from previous calculations is the active surface area per gram of sample material AA and, from the catalyst manufacturing procedure, the fractional proportion of metal in the catalyst bulk.
The calculation employs an expression of the geometry of the grain. From the assumed regular geometry, the diameter can be expressed in terms of the area and volume. The volume of active metal is not known, although the atomic or molecular density ρm is; therefore the volume can be expressed in terms of density. The area of active metal per gram of sample was previously measured, providing a value for area per unit mass of metal Am (m2/g). Substituting these expressions into the general relationship for D = f(A,V) yields
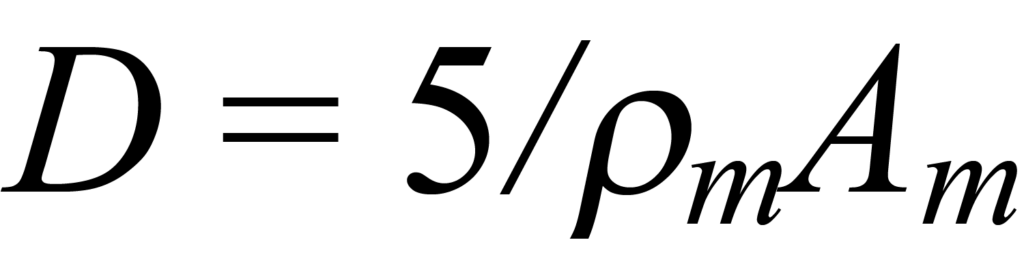
for a cubic grain on the surface (five of six faces exposed) and
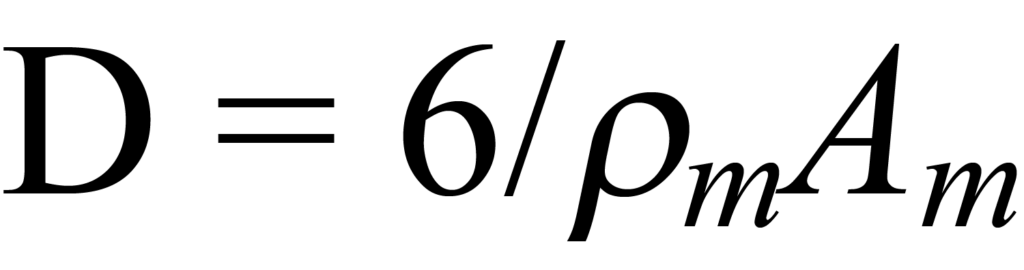
for a hemispherically shaped particle.
The diameter calculated by the above equation represents the average diameter of the active metal grains onto which adsorption occurred.
Temperature Programmed Chemisorption
As the name of the method implies, temperature programmed chemisorption is a method that involves the effects of temperature on surface reactions. There are three principal reactions that are studied as a function of temperature: 1) desorption, 2) reduction, and 3) oxidation.
Temperature-programmed desorption by the dynamic method involves placing a sample in a sample cell and pre-treating it to remove any adsorbed species from the active surface. Next, a selected gas or vapor is chemisorbed onto the active sites until saturation is achieved, after which the remaining adsorptive molecules are flushed out with an inert gas. Temperature (energy) is increased at a controlled rate while a constant flow of inert gas is maintained over the sample. The inert gas and any desorbed molecules are monitored by a TCD. The TCD signal is proportional to the quantity of molecules desorbed as thermal energy, monitored by a thermocouple, overcomes the binding energy. Quantities desorbed at specific temperatures provide information about the number, strength and heterogeneity of the adsorption sites. Analysis data are usually plotted as quantity desorbed versus temperature, or as both temperature and quantity desorbed plotted over time.
Figure 5 is a typical TPD profile of hydrogen desorption from Pt supported on Al2O3 . The first peak is obtained at a temperature of 393 K. This peak corresponds to the weak adsorption of hydrogen and may relate to desorption from the support or from weak chemisorption. The second peak obtained at the next higher temperature (493 K) probably corresponds to hydrogen spillover due to the presence of Pt on alumina. The third and final peak obtained at 570 K corresponds to the hydrogen chemisorbed by Pt. This peak is quantified to estimate the quantity of Pt available for catalytic activity in a reactor. Binding energies can be quantified using the TPD method as will be discussed subsequently.

Temperature-programmed reduction is a method by which a reducing gas mixture such as hydrogen diluted in an inert gas flows over a sample of an oxide. The initial temperature is usually below the reduction temperature. Next, sample temperature is increased at a constant rate and, as reduction begins, hydrogen is consumed from the carrier mixture, which is detected by a TCD. When reduction ceases, no more hydrogen is consumed and the thermal conductivity of the gas from the sample tube returns to baseline. Several reduction peaks may be detected over the course of the temperature ramp because reduction likely will be initiated at various thermal energy levels. Each peak then corresponds to a different oxide and the amplitude of each peak is proportional to the reaction rate.
Iron oxide in the form of hematite exhibits three phases of reduction corresponding to the three oxides of iron. A TPR analysis of hematite was performed using a reducing gas composed of 10% hydrogen in argon and a temperature ramp rate of 10 °C/min. Figure 6 shows the results. The first reduction peak appears at 575 K, corresponding to the transition of Fe2O3 to Fe3O4. The peak at 627 K corresponds to the transformation of Fe3O4 to FeO. The final peak at 748 K corresponds to the transition of FeO to Fe. The positions of the maxima shown in Figure 6 may differ somewhat from sample to sample depending on the particle size of the Fe2O3 and other parameters such as temperature ramp rate.
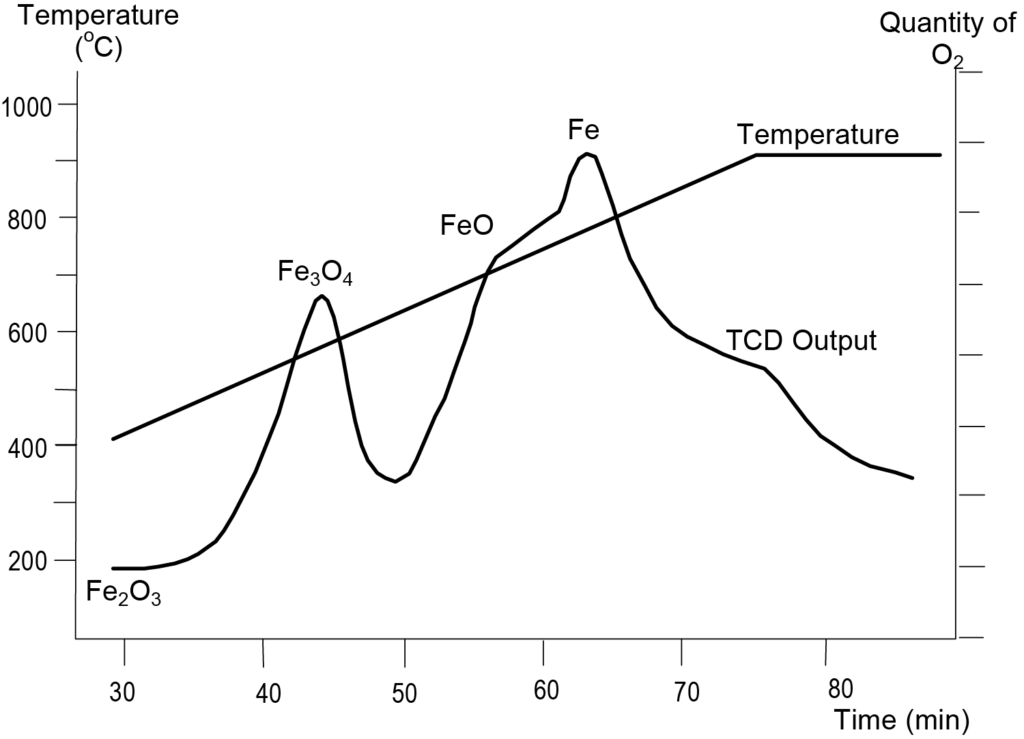
Temperature-programmed oxidation may be used to determine the quantity of reduced species (also called degree of reduction), but the difficulty with this type of analysis is in attaining total oxidation. More commonly, TPO is used in applications such as the study of the kinetics of coking, evaluation of catalyst carbon burn off, determination of the different forms of carbonaceous deposits present on the catalysts after a CO decomposition reaction or, stated more generally, measurements of oxygen consumption and product yields.
The sample is heated at a uniform rate as the reactant gas, typically 2% to 5% oxygen, is applied to the sample in pulses, or alternatively, as a steady stream. The oxidation reaction occurs at a specific temperature resulting in an uptake of oxygen. The amount of oxygen consumed during the reaction is related to the quantity of a species on the surface.
Surface Energy and First Order Kinetics
Adsorption and desorption mechanisms are composed of some combination of elementary kinetic steps. For example, a diatomic molecule can be adsorbed or, as it approaches the surface, it may fragment into atoms that are adsorbed independently. The former case is called non-dissociative chemisorption or first-order kinetics, the latter is dissociative chemisorption or second-order kinetics. First-order kinetics will be of primary focus in the following discussions.
The interaction of a single, isolated molecule with a surface can be depicted in a plot of potential energy versus distance from surface as in Figure 7. For comparison, Figure 7 also includes an energy plot for physisorption as well as the net energy path taken by the chemisorbed molecule. It should be understood while examining this diagram that it is a basic depiction of a single molecule approaching a surface and considers only energy as a function of distance from the surface, neglecting other variables.
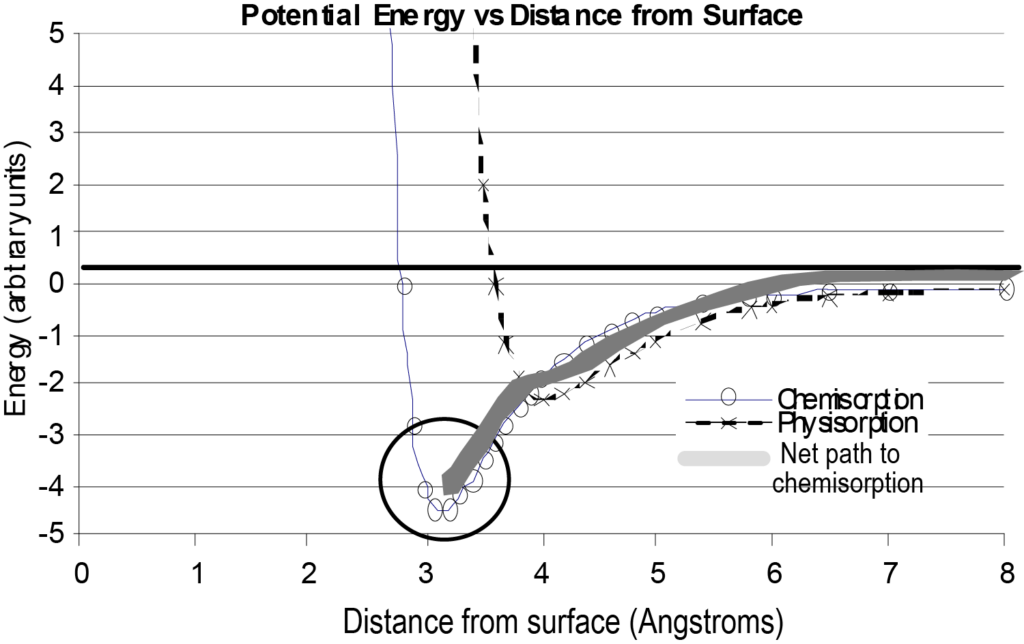
One situation that would greatly change the shape of the chemisorption curve in Figure 7 would be if the adsorption process were to be dissociative. Dissociative chemisorption requires an expenditure of energy (dissociation energy) to fracture the adsorptive molecule. This would result in the net energy path having a positive peak just before the negative-going potential energy well. This is illustrated in Figure 8. As in Figure 8, the physical adsorption path initially is more favorable (lower energy) as the molecule approaches the surface, but to dissociate and chemisorb, a positive energy step is required to make the transition to the chemisorption path. This energy is in excess of the dissipated potential energy of the molecule.
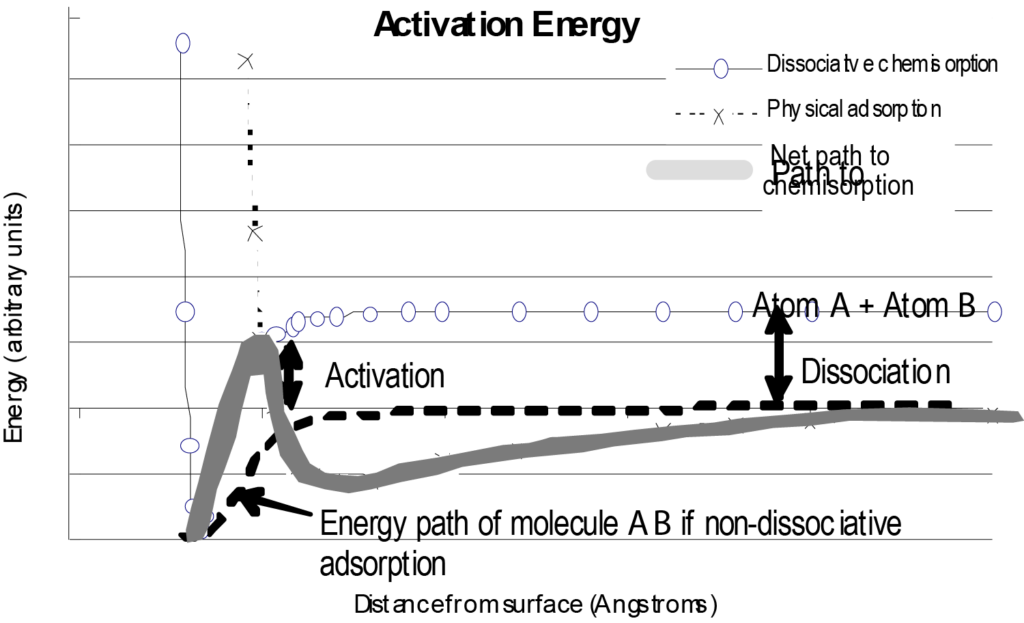
An important variable that changes the shape of the non-dissociative chemisorption energy curve is the number of molecules already adsorbed on the surface. The most energetic sites (the deepest potential wells) are occupied first. This manner of coverage continues until, finally, those sites having the lowest energy are occupied. The energy plotted as a function of surface coverage (loading) characterizes the degree of heterogeneity of surface energy. This plot provides valuable information about catalyst activity under specific conditions. For some applications, rather than a plot of surface energy distribution, a single value for the energy associated with the reaction may suffice.
Adsorption is an exothermic process, thus it ultimately yields energy (energy of adsorption) even if some energy input (activation energy) is required to initiate the process. Reversing adsorption requires the input of energy, the required quantity being the depth of the potential well.
Figures 7 and 8 pertain to the potential energy of a single, isolated molecule, however it is the energy potential of all of the particles in the system that determines if the system is in equilibrium. At equilibrium, a molecule at any location in the system should experience the same energy potential; this applies to molecules in the bulk gas or vapor surrounding the solid and to the adsorbed molecules at the solid surface.
For a specific adsorbate-adsorbent system, adsorption equilibrium is achieved by a delicate balance between the pressure P of the bulk gas phase, analytical temperature T, and the degree of surface coverage ϑ. Experimentally, one of these parameters is held constant, the other is assigned a value, and the third is observed to determine its value at equilibrium. An isotherm conveys the degree of surface coverage as a function of pressure at constant temperature (ϑ = f(P)T), an adsorption isobar expresses the degree of surface coverage as a function of temperature at constant pressure ϑ = f(T)P), and an isostere shows the relationship between pressure and the temperature for a constant degree of coverage. (P = f(T)ϑ).
The Clausius-Clapeyron equation expresses the heat of adsorption at a specific degree of surface coverage ϑ in terms of pressure and temperature, thus it yields the isosteric heat of adsorption qst. The equation in partial differential form is
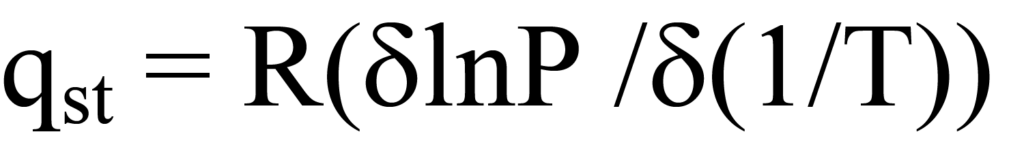
where T is temperature, P pressure, and R the gas constant.
Obtaining related values of temperature and pressure for a given degree of coverage is achieved by obtaining multiple isotherms of the same sample at different temperatures and scaling the quantity adsorbed axis in units of degrees of coverage. This provides a means for extracting from the set of isotherms, a set of isobars plotted as degree of coverage versus temperature over the range of temperature used in the analyses. From the set of isobars, a set of pressure versus temperature values for various values of values of volume adsorbed can be extracted. These are plotted as ln(P) vs. 1/T.
The Clausius-Clapeyron equation, above, can be regrouped in linear form, y = m(x), yielding
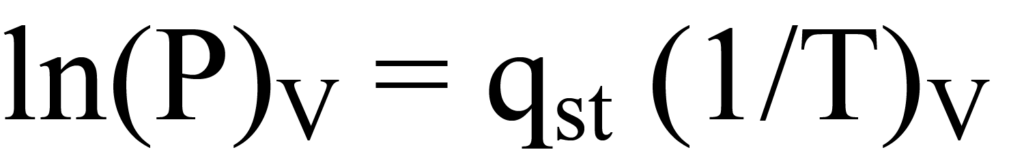
R being a scaling constant that does not affect the slope. For value of quantity adsorbed, there is a different slope, qst. Plotting the set of slopes as a function of quantity adsorbed provides the sought-after graph of surface energy versus quantity adsorbed, which relates to surface coverage or loading.
Heat of adsorption also can be calculated from data obtained by dynamic chemisorption by what is sometimes called the ‘heating rate variation’ method. Since quantity adsorbed as a function of pressure is not monitored by the dynamic method, an expression of energy other than those of Eqs. 10 and 11 must be sought. As an exercise, such an expression is derived in the following paragraphs. The result (Equation 21) can be taken and used on faith and the drudgery of wading through the math avoided. However, the step-by-step derivation is presented here because it may be of interest to some readers and a detailed derivation is difficult to find in the literature. Portions of what follows were gleaned from works of Schroeder and Gottfried, Houston, Nix, and Garrett.
Desorption involves the time rate of change of the number of adsorbed molecules N, algebraically expressed as ΔN/Δt. This also may be viewed as the time rate of change in the number of available adsorption sites Na.
(Note: Time-dependent and temperature-dependent changes are more conveniently dealt with mathematically by considering each step change in time or temperature to be infinitesimally small. Thereby, DN/Dt can be replaced by ΔN/Δt and algebraic manipulation is replaced by differential calculus. For readers not familiar with calculus, any expression of the form dX/dY can be considered to be the slope of a plot of X versus Y at a given value of X.)
The kinetic expression for the rate of desorption Rd is
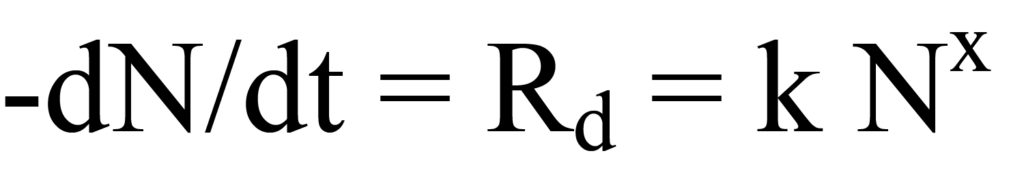
where k is the rate constant, -N the instantaneous surface concentration (number) of the adsorbed species (negative indicating decreasing), and x the kinetic order. Only the simplest case, first order (nondissociative) kinetics, is considered here; therefore x=1. Note that the rate of desorption constantly changes as the number of molecules remaining on the surface diminishes.
Figures 8 and 9 illustrate that activation energy may or may not be required to cause adsorption to proceed. However, these figures also illustrate that there always is an activation barrier that must be overcome for the molecule to desorb, that is, for the chemisorption surface reaction to reverse. The relationship between the rate constant and energy in energydependent reactions such as desorption can be expressed in an Arrhenius form, specifically
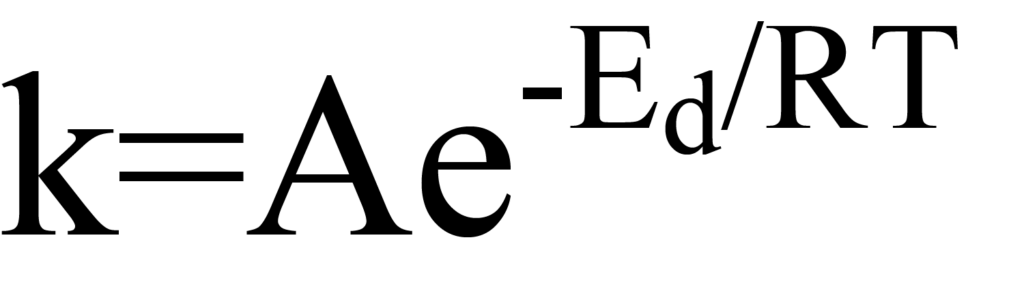
where Edes is the activation energy and the subscript ‘d’ identifying the particular case as that of desorption. The pre-exponential factor A can be considered the number of attempts by the molecule per unit time to escape from the potential well. T is temperature (degrees Kelvin) and R the universal gas constant. The product RT is thermal energy, so the exponent E/RT is the ratio of activation energy to thermal energy. While E is larger than RT, there is little probability of desorption.
Substituting the Arrhenius expression into Eq. 8 gives
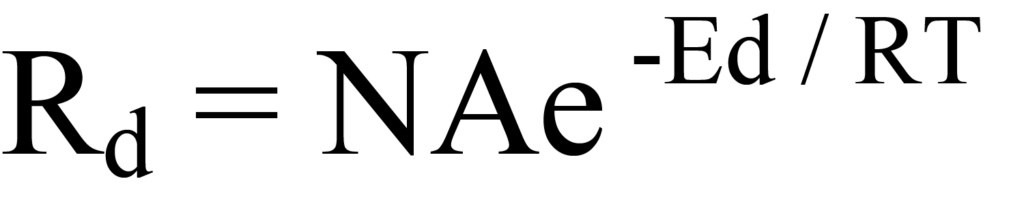
This is the Polanyi-Wigner equation for rate of first-order desorption. One can experiment with this equation to better understand what it describes in regard to desorption How desorption rate (Rd), coverage (N) and the energy ratio (Ed/RT) change as a function of temperature are plotted in Figure 10, the values being normalized on the vertical axis for convenience. During an actual experiment the detector output would correspond to the rate of desorption. The temperature Tm at which the rate of desorption is maximum is easily observed in Figure 10 as it would be on a plot of detector signal (quantity of evolved molecular species) versus temperature.
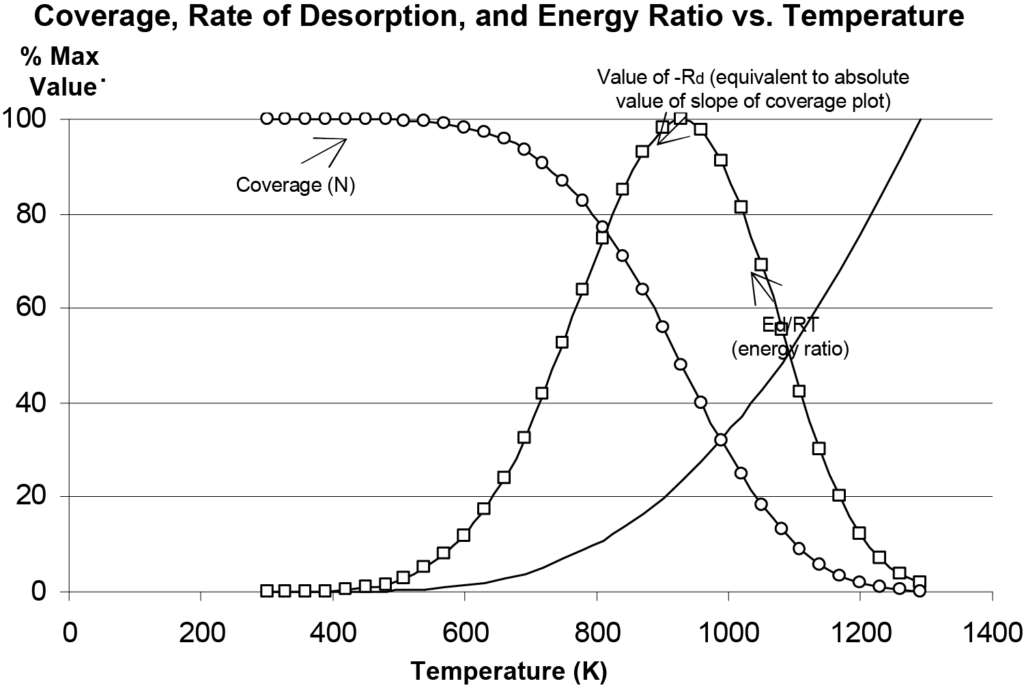
Note: Figure 10 was produced by Microsoft Excel® using Eq. 14 and arbitrary values for the parameters. This allows experimentation with the parameters and comparison of various plots predicted by the Polanyi-Wigner model. It can be observed that peaks are somewhat asymmetric around Tm, increasing the initial coverage value causes the peak to increase in amplitude but with Tm remaining constant. Increasing the value of A causes the peak to move towards lower temperatures. Increasing Ed causes the peak to broaden and the maximum value occur at higher temperatures.
Extracting the log of both sides of Equation 10 produces
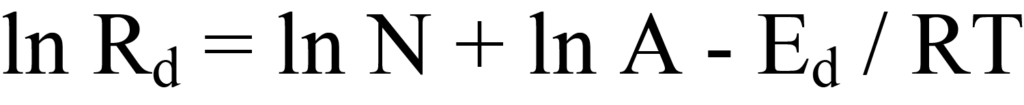
Grouping this equation in linear form, y = (m)x +(b) yields
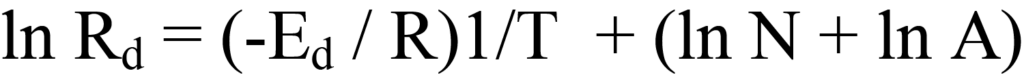
Plotting ln Rd versus 1/T produces a straight line having slope -Ed/R and intercept (ln N + ln A). The problem, here, is that numerical values for Rd are not available, so the derivation must be expanded.
During a temperature-programmed analysis test, the sample is heated linearly so that the temperature T at any time t can be calculated by
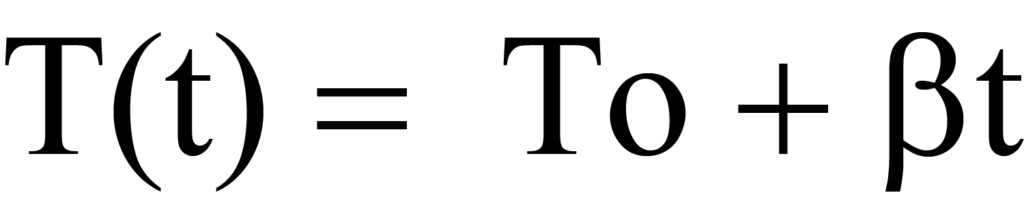
or
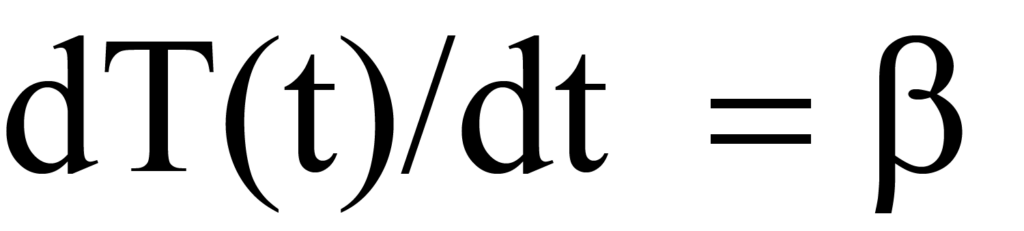
where β is the heating rate or ramp rate dT/dt in units of degrees K per unit time. As temperature is increased, there is a change in the number of molecules being desorbed per unit time, expressed by dN/dT. Multiplying the time-dependent heating rate (dT/dt) in degrees/min by the temperature dependent rate of desorption (-dN/dT) in molecules/degree) gives timedependent rate of desorption, Rd. Mathematically,
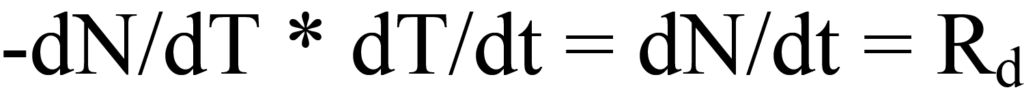
Heating rate β was defined in Eq. 15a as dT/dt, therefore, substitution into the left side of Eq. 12 gives
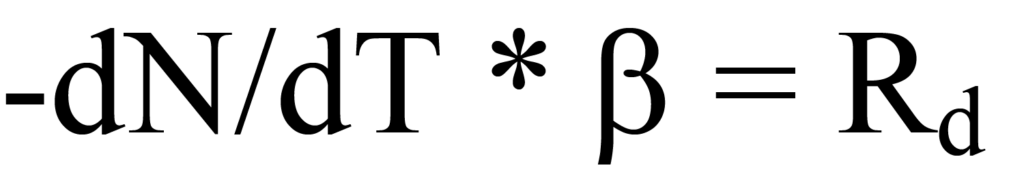
Substitution of Eq. 17 into Eq. 14 yields
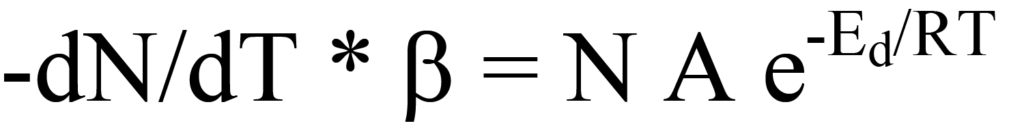
and rearrangement yields the temperature-dependent rate of desorption,
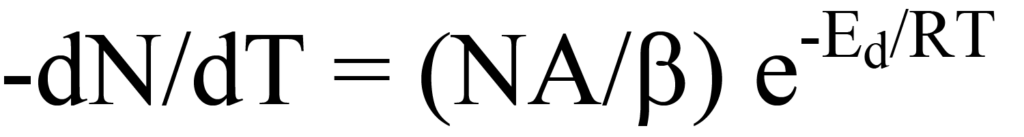
which describes the rate of desorption plot in Figure 10. As temperature increases, the rate of desorption maximizes at Tm and at that temperature the slope (first derivative) of Eq. 15 equals zero, that is,
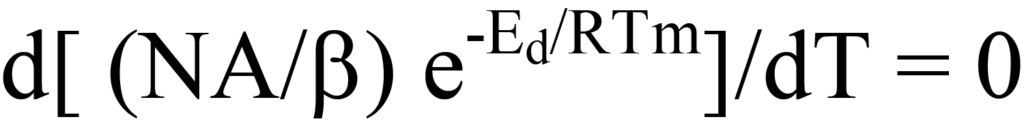
For clarity and continuity, the reader is reminded that Equation 20 has the form d(uv)/dT, where u = (A/b)N, v = e-Ed/RT, and N is a function of temperature (T).
Equation 20 yields
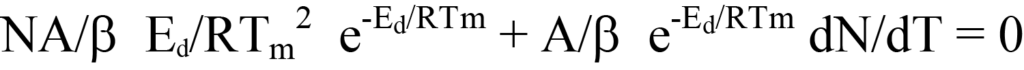
Now, substitute the right side of Equation 19 for dN/dT (a negative value; see Equation 12) in Equation 13 and factor. This gives
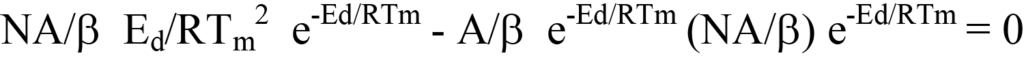
or
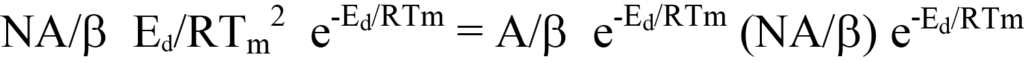
Eliminate common terms on left and right sides, and there is left
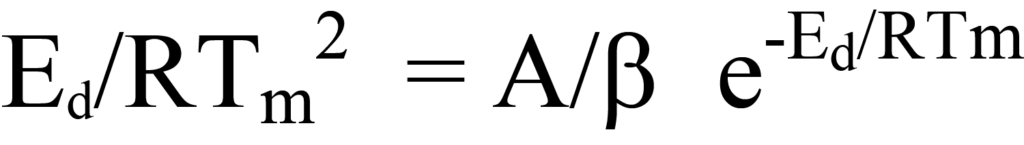
The values of Tm, β, and R are known; A is unknown as is Ed, the value which is sought. One approach to determining the unknowns is to express the terms of Equation 23 in linear form, y = mx + b. This can be done by rearrangement to
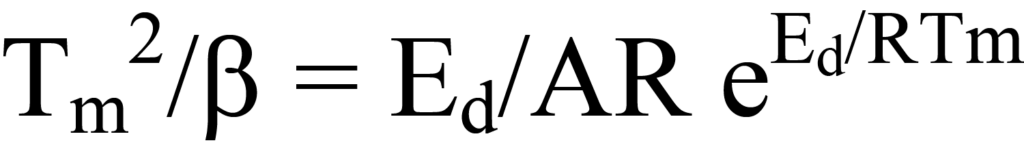
Taking the log of each side yields

a linear equation in which y = ln Tm 2/β, x = 1/Tm , m = Ed/R, and b = ln Ed/AR. Plotting y versus x for a series of β values allows the determination of Ed. Another form of Equation 25a sometimes found in the literature follows from expanding the logarithmic terms to obtain
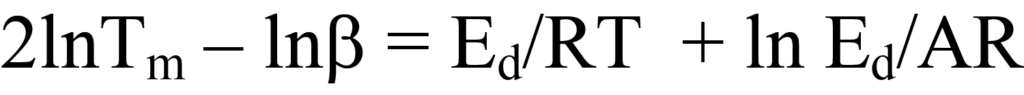
Another way to arrive at Equation 25 from Equation 22a is to factor and rearrange the latter equation, giving
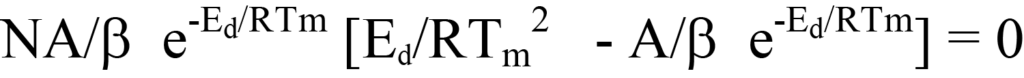
Dividing both sides of this equation by the expression in the brackets gives
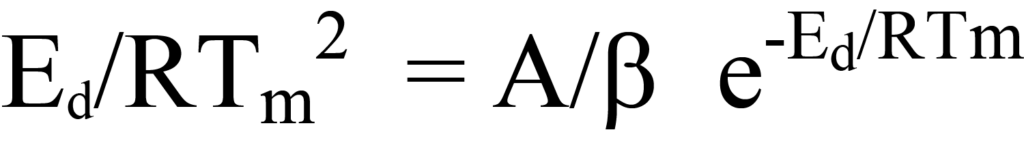
which is the same as Equation 23.
There also is the case
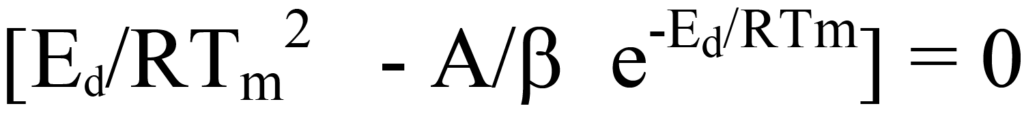
or
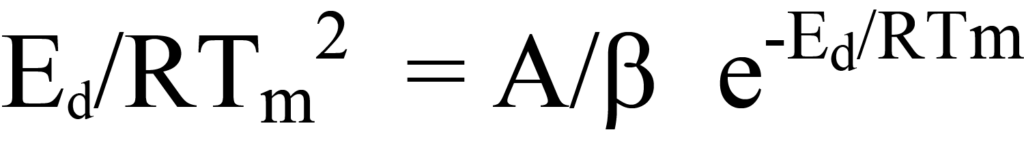
established by dividing both sides of Equation 26 by the factors outside of the brackets or by logically deducing that since neither factor NA/β nor e-Ed/RT has a value of zero during the desorption process, the expression in the brackets of Equation 26 must equal zero. Rearranging yields
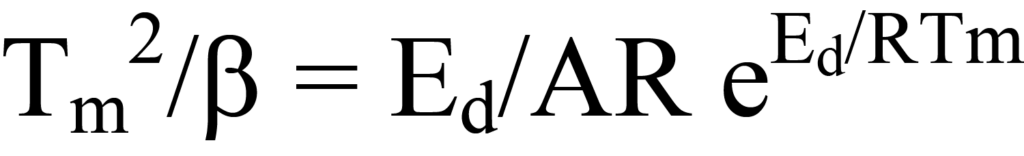
which is the same as Equation 24.
Following the method of Redhead, Equation 25 is rearranged as follows:
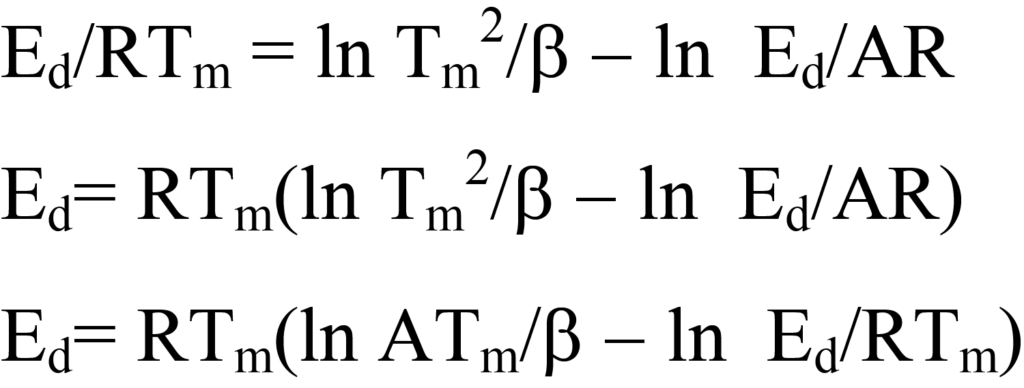
This equation is simplified by estimating the ln Ed/RTm term on the right side to be 3.64, which introduces an error of less than 1.5% for values of A/β between 108/K and 1013/K, A typically being approximated for first order kinetics to be 1013/s. Thus,

Much like the single point method of determining BET surface area, this method introduces some error, but it allows Ed to be estimated from a single desorption chromatogram. (Schroeder and Gottfried). Rather than estimating the value of A, a series of chromatograms could be obtained for different values of β and the values of Ed and A determined from the linear plot.
In using the Redhead method, it must be remembered that it applies only to first order kinetics. In regard to higher order reactions, Stoltz admonishes (Stoltze), “To describe E obtained in this fashion as an approximation is an understatement, completely wrong is a better description.”
Summary
Solid catalysts play a ‘behind the scenes role’ in making affordable and even making possible many of the benefits enjoyed in everyday life. Chemisorption is a fundamental step in catalytic reactions, so being able to study the chemisorption process on a small scale in the laboratory is of great benefit. Modern analytical instruments capable of characterizing these reactions are powerful tools for monitoring and controlling the manufacture and application of catalysts and predicting performance characteristics of newly developed catalyst materials.
Resources
James P. Olivier, Thermodynamic Properties of Confined Fluids I: Experimental Measurements of Krypton Adsorbed by Mesoporous Silica From 80K to 130K, The 2nd Pacific Basin Conference on Adsorption Science and Technology, University of Queensland, Brisbane, Australia, May 2000.
Sven L.M. Schroeder and Michael Gottfried, Temperature- Programmed Desorption (TPD) and Thermal Desorption Spectroscopy (TDS), Freie University, Berlin (Internet http://userpage.chemie.fuberlin. de/~pcfp/V18/pdf/v18.pdf).
Paul L. Houston, Cornell University Chemical Kinematics and Reaction Dynamic, Ithaca.
Roger Nix, An Introduction to Surface Chemistry, Department of Chemistry, Queen Mary University of London (World Wide Web http:// www.chem.qmw.ac.uk/surfaces/scc/scat2_4.htm).
Simon J. Garrett, An Introduction to Surface Chemistry (lecture notes) , Michigan State University.
W.J. Moore, Physical Chemistry, Prentice-Hall, Inc. (1972).
J.H. de Boer, The Dynamical Character of Adsorption, Oxford at the Clarendon Press (1953).
G.C. Bond, Heterogeneous Catalysis- Principles and Applications, Claredon Press, Oxford (1987).
John H. Sinfelt, Structure of Metal Catalysts, Review of Modern Physics, Vol. 51, No. 3 (1979).
Thomas H. Maugh, Industry Steps Up Quest for Catalysts, High Technology, August 1984.
Scholten, Pijpers and Hustings, Surface Characterization of Supported and Nonsupported Hydrogenation Catalysts, Catal. Rev.–Sci. Eng., Vol. 27, No. 1, (1985).
A. Baiker, Experimental Methods for the Characterization of Catalysts. II. X-Ray Diffraction, Temperature- Programmed Desorption and Reduction, Thermogravimetry and Differential Thermoanalysis, International Chemical Engineering, Vol. 25, No. 1 (1985).
Philip Moriarty, Atoms and Molecules at Surfaces, School of Physics & Astronomy, University of Nottingham ( World Wide Web http:// www.nottingham.ac.uk/~ppzpjm/sect4_2.htm).
M. B. Raschke, U. Ho, Chemisorption energy of hydrogen on silicon surfaces, Physical Review B, Volume 63.
P. A. Redhead, The Ultimate Vacuum, Vacuum 12, 203-211, 1962.
Per Stoltze, Introduction to heterogeneous catalysis- Concepts and calculations, Department of Physics, Technical University of Denmark.
Gerard P. van der Laan, Kinetics, Selectivity and Scale Up of the Fischer-Tropsch Synthesis, Doctoral Thesis, University of Groningen, The Netherlands, 1999.