The AccuPyc 1330 Series pycnometers allow you to enter a sample mass (weight) determined to four decimal places. Four decimals are sufficient even when working with small sample masses; it is not necessary to use additional decimal places. This application note explains why.
Density of a material is defined as the mass of material per unit volume. In the case of gas pycnometry, the sample mass is determined using a balance and the sample volume is determined using a pycnometer, such as an AccuPyc 1330. The operator enters the sample mass and the AccuPyc calculates the density, D, after measuring the volume, using the equation:
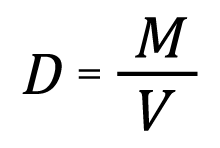
where M is the sample mass measured using a balance and entered by the operator, V is the sample volume measured by the AccuPyc.
Since the density is calculated from two independently measured parameters, the expected error in the calculation results from a combination of errors in the two individual measurements. Since the density is calculated by division, the individual relative errors of the two measured quantities are added to give the density relative error (in order to calculate the combined error in the density result). The relative error is the actual error divided by the actual measured or calculated values, or:
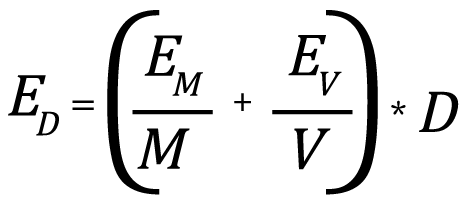
where EM is the maximum expected error in the measured sample mass, EV is the maximum expected error in the measured volume, and ED is the maximum expected error in the calculated density. To see how this works, let’s take a look at some examples.
Start with a low density sample, perhaps an organic powder. Typical density for this type of material is 1.0g/cm3. Using the AccuPyc with 1cm3 capacity, fill the cup with the powder (0.7cm3 maximum). This sample would have a mass of approximately 0.7g. Assume that the weight is measured to be 0.70000g and that the volume of the sample measured by the AccuPyc is 0.7000cm3. Now, what are the expected errors for mass, volume, and density?
The accuracy specifications for the AccuPyc are:
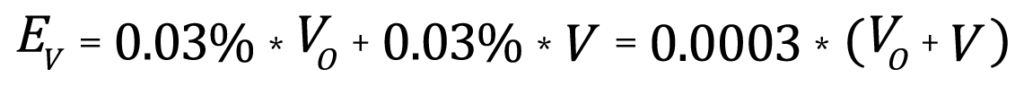
where VO is the full scale capacity of the AccuPyc (1.0000cm3 in this case), V is the measured sample volume (0.7000cm3 in this case), and EV is the expected maximum error in measurement. For this example, the expected error is 0.00051cm3 or less. Dividing this error by the measured value gives the maximum relative error in the volume measurement, expressed as a percentage, of 0.073%.
For this mass error, assume that the balance is accurate to 1 in the fifth decimal place. In this case, the
expected error is 0.00001g or less. For the sample weight measured, 0.70000g, the maximum expected
relative error is 0.0014%.
Adding these two relative errors gives the maximum expected relative error in the calculated density, 0.074%. Multiplying this by the measured density, 1.0000g/cm3, gives the maximum error in the density measurement, 0.00074g/cm3. Notice that almost all of the density error, 98% of it, results from error in the measured sample volume alone.
This calculation assumes that weight could be entered to five decimal places. Since the AccuPyc allows entry of only four decimal places, how does this affect the expected maximum error in the calculated density?
For this example, assume a maximum mass error of 1 in the fourth decimal place, or 0.0001g. This time, the relative error in the mass entered into the AccuPyc is 0.014%, ten times larger than before. Since we are talking about the same volume measurement capabilities, the maximum expected relative volume measurement error is still 0.073%. Now the calculated maximum expected density error, with only a four-decimal place entry, becomes 0.087% g/cm3. Even with only a four decimal place entry, 84% of the total error results from error in the volume measurement. If we could enter mass to five places instead of four, for this 1.0000 g/cm3 sample, our density accuracy would improve from 0.087% to 0.073%, or roughly 2 in the fourth decimal place for density. Actually, this is not much of an improvement when you compare the cost of balances with four-versus five decimal place resolution.
In another example, try working at the low end of the specified capacity for the AccuPyc, namely 10% of the full scale volume. This means using only 0.1000cm3 of the sample, which we would expect to weigh 0.1000g. (A density of 1.000g/cm3 is still assumed.) This time, the maximum expected error in the volume measurement is 0.00033g/cm3, or as a percentage of the measured value, 0.33%, quite large since the sample cup is almost empty. The expected maximum error in the measured mass, for five decimal places, is 0.00001g, or 0.01% of the measured mass. If using only four decimal places, the mass error potentially increases to 0.0001g, or 0.1%. Combining volume and mass errors gives 0.34% and 0.43% relative error in the density calculation, for five and four decimal place mass entry, respectively. Since the measured density is 1.000 g/cm3, this amounts to a difference of only 9 in the fourth decimal place in the calculated density! You can see that the volume error still accounts for most of the total error, 97% with five decimal place entry, and 77% with only four.
This is a worst-case scenario, with minimum volume in the AccuPyc sample cup and low sample density. To illustrate this, suppose you are analyzing a high density sample with a density of 4.0000 g/cm3. Using calculations like the ones performed above, you would have the following expected error in density.
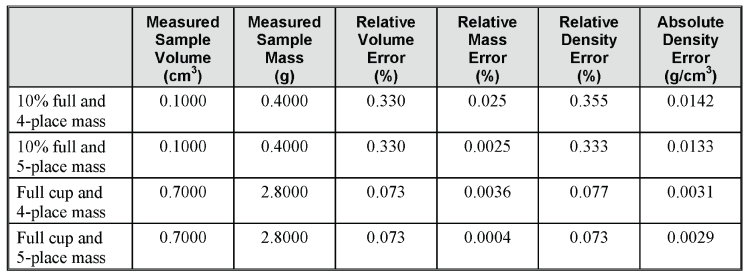
Again, notice that the difference in density error, due to weighing to four versus five decimal places, is 2 or 9 in the last decimal when the sample cup contains 70% or 10% of the full scale capacity, respectively. Once again, most of the error is due to error in the measured volume. For an even greater example, compare the maximum relative errors for materials with different densities, from 0.8000 to 20.0000g/cm3, assuming a weighing error of 1 in both the fourth and fifth decimal places, and for 0.7000, 0.4000, and 0.1000cm3 of the sample.
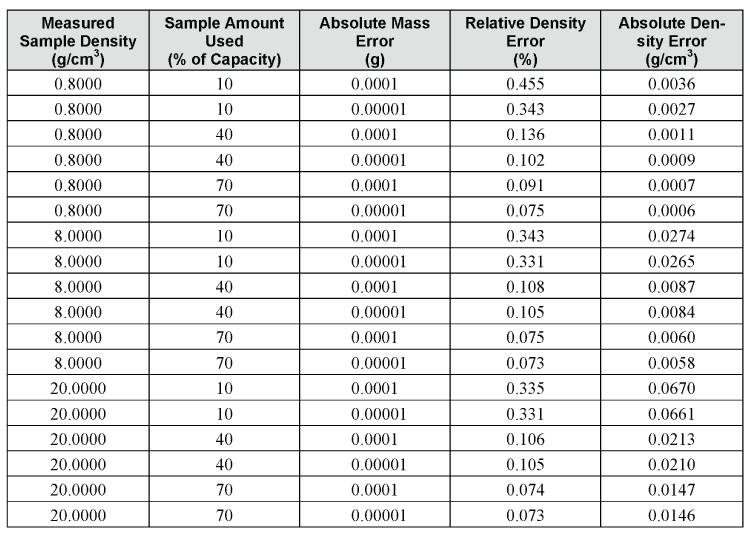
To summarize, adding the capability for a fifth decimal place does not greatly improve the maximum expected error in the calculated density, especially if the sample cup is almost filled with the sample.